----- Original Message -----
From: Cathbleue
To: Picabiette
Sent: Sunday, July 06, 2003 2:34 PM
Subject: se trouver nez à nez ...

Je reviens sur une question que tu as posée l'autre jour pour Pascale la stylite en haut de sa colonne : Où que l'on soit, est-ce un endroit où l'on arrive, ou un endroit d'où l'on part ?

Pas de mathématiques ni de latex, mais avec l'aide de Monsieur Villemin je vais répondre simplement à cette question qui avant tout est une question liée à la relativité.


D'abord quelques principes qu'évoquent Monsieur Villemin :

[1] - Le principe de la relativité

Dans un train en allure de croisière, vous ne vous apercevez pas du mouvement, à moins de regarder à l'extérieur
Dans un train au repos, le train voisin démarre: vous avez l'impression que vous démarrez!
Qui bouge? moi ou lui?

§ Tout mouvement uniforme est RELATIF et ne peut être détecté sans référence à un point extérieur

On ne sait pas que l'on avance si on ne regarde pas dehors - Galilée (1564-1642)

[2] - Expérience classique du train

Un wagon en mouvement avec une porte à l'avant et une à l'arrière et une lampe au milieu

L'ouverture de chacune des portes est déclenchée par l'arrivée de la lumière

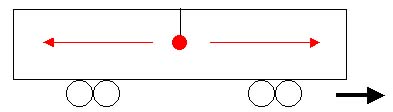
Dans le wagon : Un observateur au centre du wagon, constate l'ouverture de chacune des portes au même moment

À l'extérieur : Pour un observateur au sol, la porte arrière s'ouvre avant la porte avant comme si la porte arrière allait à la rencontre de la lumière, tandis que la porte avant s'en éloigne

Distance : Si la personne au centre du wagon va vers la porte avant , pour lui, il parcoure 1/2 L (Longueur du wagon), pour le gars dehors, il parcoure 1/2 L + une certaine distance parcourue par le wagon pendant ce temps

Logique non!
La distance parcourue est une notion relative

(d'autres détails sont là)

Alors Où que l'on soit, est-ce un endroit où l'on arrive, ou un endroit d'où l'on part ?
Eh bien tu le vois mouvement et distance sont des notions relatives, que l'on soit dans un train, en haut d'une colonne ou bien à Vitry Sur Seine - RER C - Bus n°180.

Tant que la vitesse de la lumière est une constante qu'importe d'arriver ou de partir !

La démonstration ne serait complète sans ces extraits de Pierre Dac, qui à eux seuls auraient suffit